Introduction to Washer Method Calculator
The volume of revolution calculator is an online tool that helps you to calculate the volume of the revolution of a solid object that has an inside hole. It is used to get the solution of the volume enclosed in two curves over a bounded region.

If you are looking for a reliable solid of revolution calculator, then you can use our volumes by slicing calculator to find a hollow structure shape volume without any error.
So, Washer method calculator help you to calculate volumes of solids of revolution of a solid object that has an inside hole. Additionally, if you would calculate the volume of spherical objects that rotate in two or three dimensions that have no inside hole, you will use our disk method volume calculator.
What is the Washer Method?
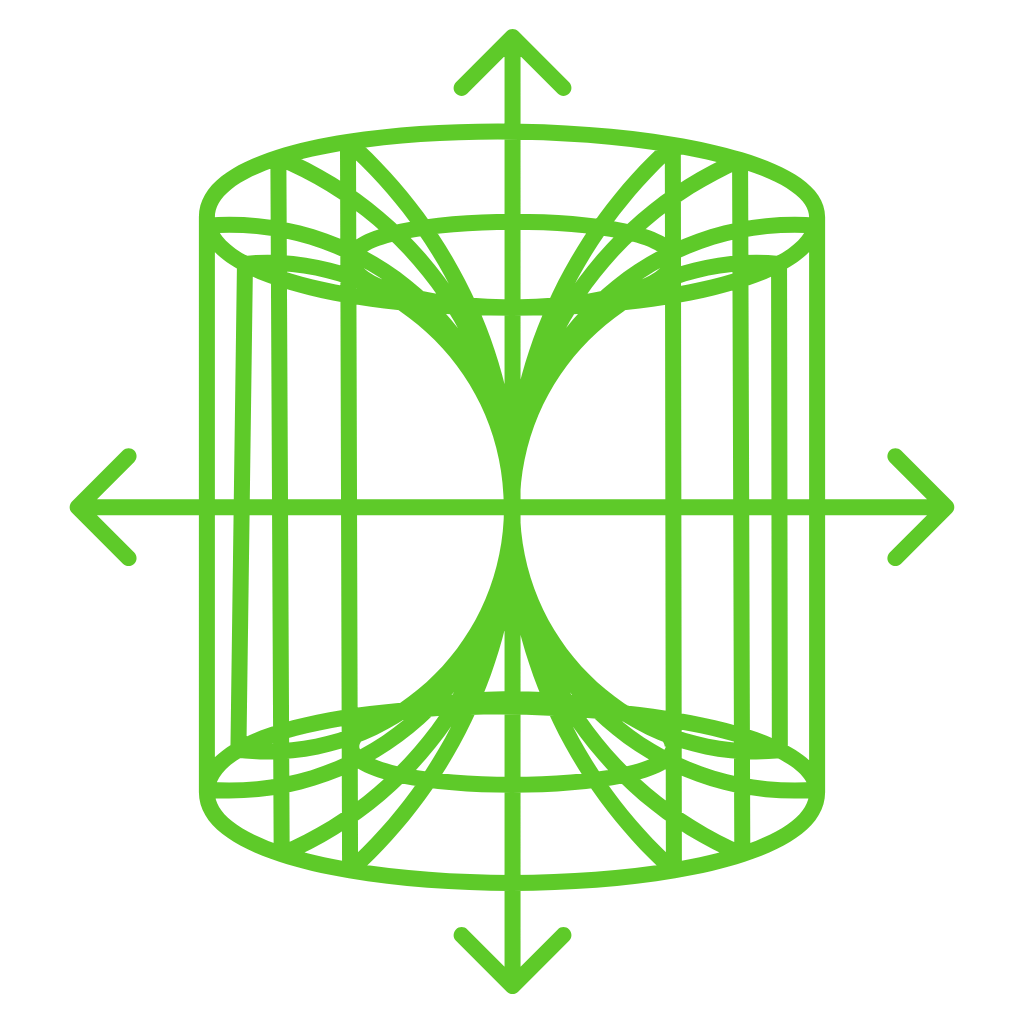
The washer method is defined as the method of the volume of solids that revolves around two curves along the x-axis and y-axis in a bounded region. It involves subtracting the volume of an inner solid from the volume of an outer solid, both of which resemble washers.
This method is particularly useful when the solid has a hole or void inside it, allowing for accurate volume computations. Additionally, for computations involving alternative methods, such as the Shell Method, you can use our volume by shells calculator for efficient volume calculations.Our calculator also provides a comprehensive solution for finding volumes of solids of revolution by integrating cylindrical shells along a given axis, offering versatility in solving various geometric problems.
Formula used by the Volume of Revolution Calculator
The washer method is represented by a volume V. The formula used by the washer calculator is,
$$ V \;=\; \int_{a}^{b} \Biggr( \pi R^2 - \pi r^2 \Biggr) dx $$
Where,
R represents the outer radius, and r shows the inner radius.
a,b is the upper and the lower limits.
dx is the thickness of the solid along the x-axis.
How to evaluate in Washer Method Calculator
The washer volume calculator provides an online way to evaluate the various kinds of solids that are present in circular shapes with internal holes because it has a built-in washer method formula and integral rules.
When you give all the values in our washer method formula calculator it determines the given problem using the washer method. It analyzed the function to identify the minor radius r(x) which revolved around the line, and the major radius R(x) which rotated around the whole sphere.
After recognizing the function, the integration process takes place then applying the upper and lower limits to give the solution. Let's take an example whose having inner and outer radii in an irregular cylindrical object only using our washers method calculator.
For additional numerical integration techniques and a deeper understanding of integration methods, such as the Trapezoidal Rule, you can use our trapezoid rule calculator. Our calculator also offers an alternative approach for approximating integrals and provides valuable insights into mathematical analysis and problem-solving.
Example of Washer Method
Our washer method calculator solves washer problems for you for your ease. But to understand the concept of the washer method some explanation is important and we are going to explain with an example,
Example:
$$ \pi \int_{0}^{1} \Biggr[( x - 3)^2 - ( -5 )^2 \Biggr] dx $$
Solution:
$$ \pi \int_{0}^{1} \Biggr( -25 + (-3 + x)^2 \Biggr) dx \;=\; \frac{-56 \pi}{3} \approx -58.643 $$
The steps of this solution are,
Calculate the definite integral,
$$ \pi \int_{0}^{1} \Biggr( (x - 3)^2 - 25 \Biggr) dx $$
Factorize the constants and integrate the sum term by term,
$$ \pi \int_{0}^{1} (x - 3)^2 dx + -25 \pi * \int_{0}^{1} 1dx $$
Substitute u = x - 3 and du = dx, for the integrand (x - 3)2. This will give a new lower bound u = 0 - 3 = -3 and upper bound u = 1 - 3 = -2.
$$ \pi \int_{-3}^{-2} u^2 du + -25 \pi * \int_{0}^{1} 1dx $$
The antiderivative of u2 is u3/3:
$$ \frac{\pi u^3}{3} \Biggr|_{-3}^{-2} + -25 \pi * \int_{0}^{1} 1dx $$
Calculate the antiderivative and subtract,
$$ \frac{ \pi u^3}{3} \Biggr|_{-3}^{-2} \;=\; \Biggr( \frac{1}{3} \pi (-2)^3 \Biggr) - \Biggr( \frac{1}{3} \pi (-3)^3 \Biggr) \;=\; \frac{19 \pi}{3} $$
$$ \frac{19 \pi}{3} + -25 \pi * \int_{0}^{1} 1dx $$
The antiderivative of 1 is x so,
$$ \frac{19 \pi}{3} + \Biggr(-25 \pi x \Biggr) \Biggr|_{0}^{1} $$
Calculate the antiderivative at limits and subtract,
$$ \left(-25 \pi x \right) \Biggr|_{0}^{1} \;=\; (-25 \pi) - (-25 \pi 0) \;=\; -25 \pi $$
$$ \frac{-56 \pi}{3} $$
Thus it is the final solution of our function with specific limits. Further, to delve deeper into numerical integration techniques like Simpson's Rule, which can be used to approximate integrals like the one above, you can use our the simpson's rule table calculator. Our calculator provides an alternative method for obtaining accurate results when dealing with complex functions or regions, enhancing your understanding and problem-solving capabilities.
How to use the Solid of Revolution Calculator
The washer method calculator provides a solution in detail for determining the volume using a definite or indefinite integration process in simple steps. These steps are:
Additionally, If you're exploring regions bounded by multiple functions and need to find the area between two curves, you would be use our area between curves calculator alongside the Washer Method Calculator for comprehensive mathematical analysis. Further, If you come across situations where you need to calculate both the volume of a rotated shape and the area between two curves, using both calculators together can help you understand the shapes better and make your calculations more precise.
- Enter an equation in the form of the outer radi f(x) and inner radi g(x) in their respective box.
- Enter the upper and the lower limit values.
- Review the given function before you press the calculate button.
- Press the “Calculate” button to get the result of the solid objects problem.
The obtained result from Volumes by Slicing Calculator:
After putting all the inputs in the washer method calculator, it shows the output as per the given function with some more options. It may include:
- In the first box, a definite result is in the number value.
- Possible step solution of a definite integral.
- In the same way, indefinite solution and its possible steps of integration.
- Press “Recalculation” to get more evaluation of shell method problems.
Why do you need the Washer Method?
In calculus, for basic shapes like cylinders, spheres, and cones, there are formulas for the volumes of circular shapes but for internally hollow objects there is no specific formula. However, the washer method is particularly useful for finding volumes of more complex shapes that cannot be explained in a single rule.
The washer method gives the formula for the volume of shapes that are not perfectly round objects like a coffee cup. Our volume of revolution calculator will give a handy solution to solve complicated problems related to these types of shapes.
The Washer Method is an essential technique in calculus that enables the calculation of volumes for complex shapes, reinforces integration concepts, enhances geometric understanding, finds practical applications, and develops problem-solving skills.
Additionally, for further exploration of calculus techniques and problem-solving tools, you can also utilize the midpoint rule integral calculator, which offers additional resources for numerical integration and mathematical analysis.
Advantages of using the Washer Calculator
There are multiple advantages of using the solid of revolution calculator for solid shapes whose has an internal hole like a cup etc. These benefits are:
The Washer Method Calculator offers a convenient, accurate, and educational tool for calculating volumes of revolution using the washer method, benefiting students, professionals, and enthusiasts alike. For a similar tool that calculates Riemann sums, you can use our the riemann sum formula calculator, providing additional resources for mathematical exploration and problem-solving.
- Our washer method calculator provides step-by-step solutions within a second.
- You can use it for any device like a laptop, tablet, computer, etc
- There is no fee for the calculation of an irregular circular shape
- Our volumes by slicing calculator has a simple interface so that anyone can access it easily.
- The washer volume calculator saves time and effort in doing long calculations.