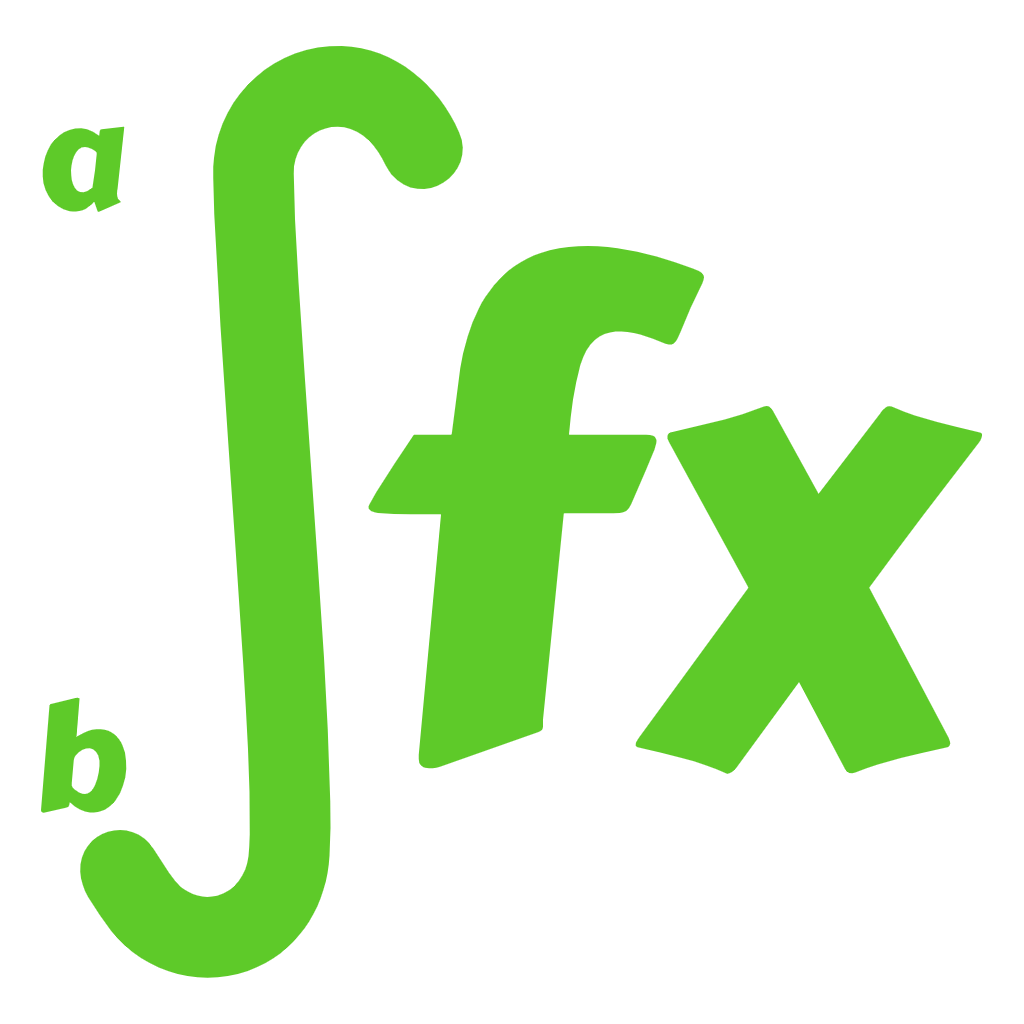Introduction to Area Between Two Curves Calculator
Area between two curves calculator with steps is an online integral tool that helps you to find the definite integral between two curves.
Area between the curves calculator evaluates finding the enclosed area between an intersecting curve in a bounded region in less than a minute. The calculator employs mathematical algorithms to calculate the definite integral of the absolute difference between the two functions over the specified interval.

It provides a convenient solution for students, engineers, and anyone dealing with curve analysis, eliminating the need for manual integration and facilitating accurate area computation. Additionally, For more advanced calculations involving volumes of revolution, you can use our volume by disks calculator. Our calculator also facilitates the computation of volumes of solids formed by rotating a region bounded by two curves about a horizontal or vertical axis, utilizing the principles of calculus.
What is the Area Between Curves?
The area between the curves is defined as the difference between two integral functions enclosed in two curves in a fixed interval in two dimensions. You can use this method to solve definite integrals only.
When graphed, these functions may intersect one another, forming regions both above and below the x-axis. The area between them represents the total area of these regions, accounting for both positive and negative areas.
This concept is widely used in calculus and real-world applications to solve problems related to finding the area of irregular shapes, determining the volume of solids of revolution, calculating probabilities in statistics, and more. For more complex calculations involving volumes of revolution using the Washer Method, you can utilize our washer method volume calculator.This tool facilitates the computation of volumes of solids formed by rotating a region bounded by two curves about a horizontal or vertical axis, providing a convenient solution for various mathematical analyses.
Formula Used by Area Between Curves Calculator with Steps:
The area between the curve formula consists of two functions in a fixed interval. The formula used by the area between two curves calculator is given,
$$ \int_a^b \biggr( f(x) - g(x) \biggr) dx $$
Where,
f(x): first function
g(x): second function
a and b: the upper and the lower limits
dx: the integral variable (along which it integrates)
Working Method of Area Between the Curves Calculator
The area between curves calculator with steps has a simple procedure that is used for the evaluation of the area between the curve functions. Our tool server has advanced algorithmic that allow it to solve different types of definite integral functions.
When you enter that function in this area between polar curves calculator, it checks the nature of the integral function and gives limits. After analyzing the given function it divides the limit into piecewise limits along with the given definite integral function.
The area between 2 curves calculator finds the upper and the lower limit of these piece-wise functions when it solves f(x) and g(x) and adds both x coordinates values.
After adding the x coordinates values in these functions, keep both functions equal to get the limit value of y coordinates. Now you have x and y coordinates values that divide the integral function in a pieces-wise limit value.
It applies the integral rule and the upper and lower limits to give the solution of a given function immediately. Now let's understand the working of the area between three curves calculator.
For further exploration into integral calculus and visualization of solid volumes, you can utilize the cylindrical shell volume calculator. This calculator aids in computing volumes of solids of revolution generated by revolving a region bounded by a curve around a line, offering a comprehensive approach to geometric problem-solving.
Example of Area Between Curve:
An example of a manual calculation of the area between curves is given below. As our area between two curves calculator with steps will determine the area between curves for you but it's crucial to know the manual calculations that are given,
Example:
Calculate the area of the region bounded by:
$$ y-2x^2 + 10,\; y - 4x + 16, x – (-2) \;and\; x - 5 $$
Solution:
$$ A \;=\; \int_{-2}^{-1} 2x^2 + 10 - (4x + 16)dx + \int_{-1}^3 4x + 16 - (2x^2 + 10)dx + \int_3^5 2x^2 + 10 - (4x+16)dx $$
$$ \int_{-2}^{-1} 2x^2 - 4x - 6dx + \int_{-1}^{3} -2x^2 + 4x + 6dx + \int_3^5 2x^2 - 4x - 6 dx $$
$$ \biggr( \frac{2}{3} x^3 - 2x^2 - 6x \biggr) \biggr|_{-2}^{-1} + \biggr( \frac{2}{3}x^3 + 2x^2 + 6x \biggr) \biggr|_{-1}^{3} + \biggr( \frac{2}{3}x^3 - 2x^2 - 6x \biggr) \biggr|_{3}^{5} $$
$$ \frac{14}{3} + \frac{64}{3} + \frac{64}{3} $$
$$ \frac{142}{3} $$
The graph of this region is given below,
Thus it is the final solution of our function with specific limits.Additionally, for exploring alternative numerical integration methods, you can use our trapezoidal sum calculator. This calculator facilitates the computation of definite integrals using the trapezoidal rule method, offering another approach to numerical integration.
How to Use Area Between Two Curves Calculator?
The area between two polar curves calculator has a simple layout so anyone can use it without any difficulty. You just need to enter the function in the calculator and the rest of the work is done in it. Follow some instructions that enable you to operate it easily.
Additionally, If you need to calculate the area using numerical methods, such as the Midpoint Rule, you can use our midpoint rule online calculator for a more accurate approximation.
- Enter the first function f(x) in this calculator
- Enter the second function g(x) in its respective box
- Add the upper and the lower limit in their respective field
- Choose the integral variable between (x,y) for a definite integral solution
- Click on the Calculate button to get the solution of the area between the curve.
- Press the Recalculate button to bring you back to the home page for more evaluation of the area between the curve.
Output from Area Between Polar Curves Calculator
The area between two curves calculator with steps gives you the outcome of your given definite integral in less than a minute. It provides you with solutions and a complete explanation. It may include as
- Result box
This box gives you a solution of the area between the curve.
- Steps
It provides you solution for the area between the curve in a step-by-step process
- Plot
Plot draws a graph according to the solution of the area under the curve.
If you need to calculate the area using numerical methods for more accuracy, such as Simpson's Rule, you can use our simpson integral calculator. This tool provides a reliable method for approximating the area under a curve by breaking it into smaller segments and applying Simpson's Rule formula.
Advantages of Area Between 2 Curves Calculator
The area between curves calculator with steps provides you with millions of advantages whenever you use it for the evaluation of integral functions that are enclosed between two curves. These advantages are:
By utilizing numerical methods or analytical techniques, the calculator ensures accurate results, eliminating the possibility of calculation errors. If you're interested in exploring other calculus concepts or numerical methods, you might want to check out our upper and lower sum calculator. This tool allows you to approximate the area under a curve using Riemann sums, providing a deeper understanding of integral calculus.
- It is a versatile tool that allows you to solve various types of integral functions.
- Our area between the curves calculator saves you time from doing lengthy calculations of the area between the curve.
- It is a free-of-cost tool you can use to find the area between the curve
- You can use this area between polar curves calculator for practice to become a pro in the area between the curve calculator
- The area between three curves calculator is a reliable tool that provides you with accurate solutions every time.
- It provides a solution with a complete process in a step-wise process.
- The area between two curves calculator with steps also provides you with a graph that helps you gain a visual understanding for more clarity about the area between the curves.