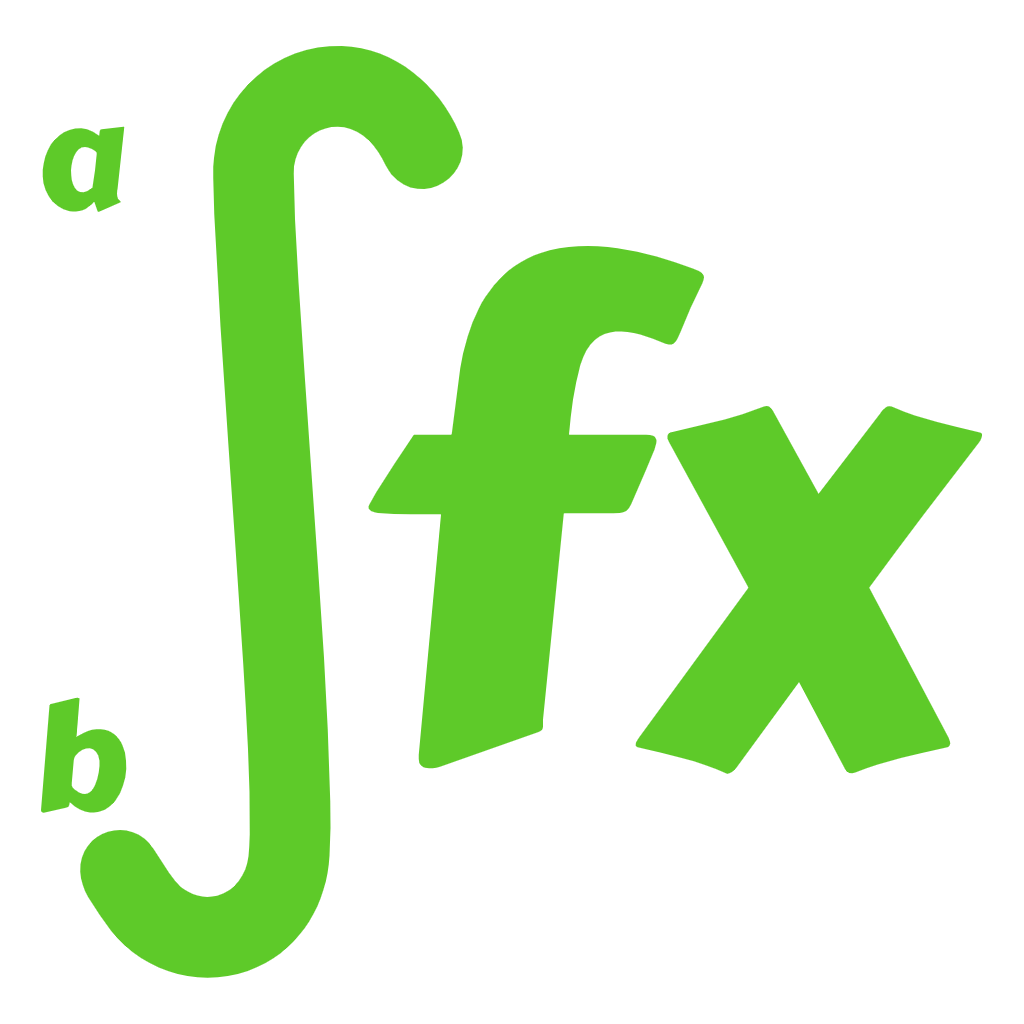Introduction to Shell Method Calculator
The Cylindrical shells calculator is a free online tool that helps to find the volume and surface area over a bounded function. It solves the definite integral of the function to determine the volume of a solid of revolution by applying the upper and lower limit values and getting results in detail in a few seconds.

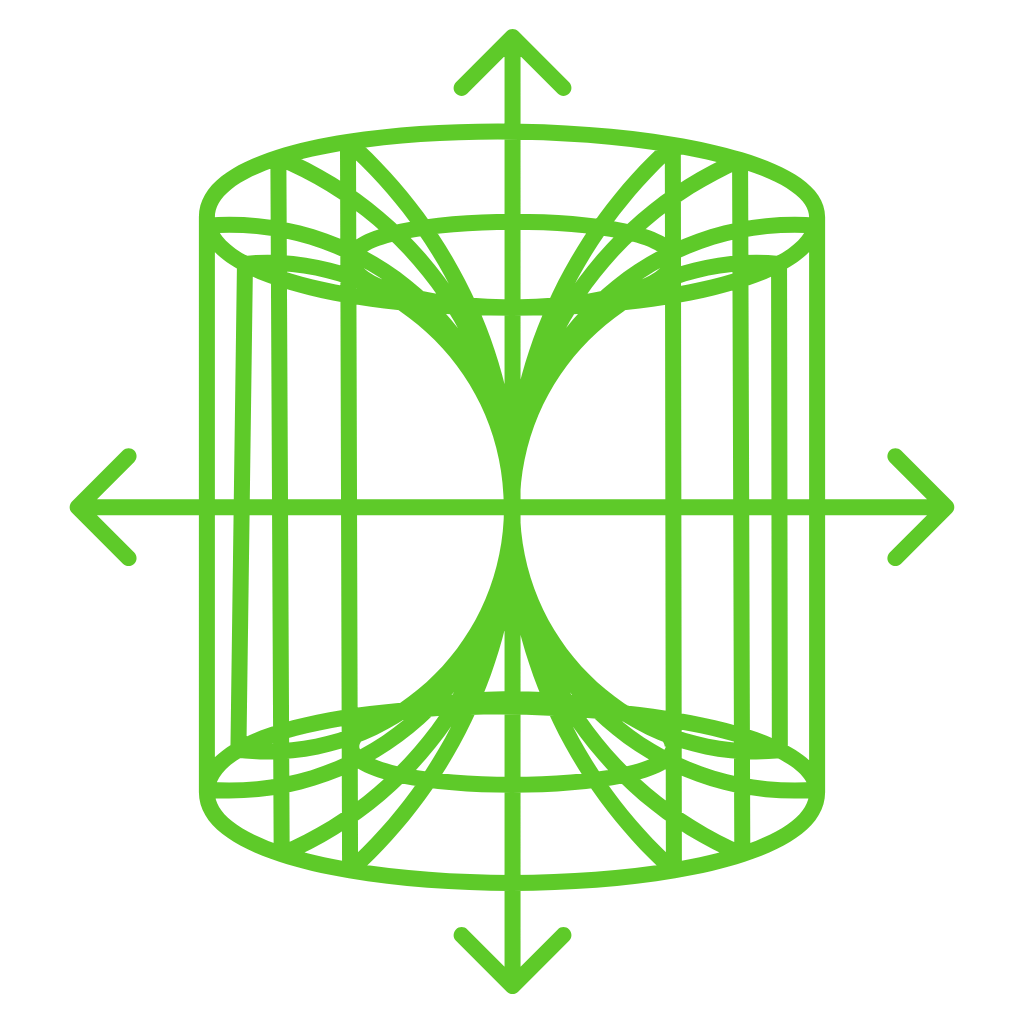
The shell method calculator is also used to compute the volume of three-dimensional solids of revolution. It employs the shell method, a calculus technique for finding volumes by integrating the volumes of infinitesimally thin cylindrical shells. Additionally, if you would like to slice the solid parallel to the axis of revolution into thin cylindrical shells. You can use our disks and washers calculator that also calculates volumes by summing the volumes of these shells, approximated as rectangular solids, using the formula 2πrhδx.
What is the Shell Method?
Shell method is a technique for calculating the volume and area of a solid object revolved in a region with definite limits is called the cylindrical shell method. It is determined through the integration process for definite functions.
The shell method is a calculus technique used to find the volume of three-dimensional solids of revolution. It involves slicing the solid parallel to the axis of revolution into thin cylindrical shells. Each shell is approximated as a rectangular solid, and the volume of each shell is calculated by multiplying its height by its circumference by its thickness
This method is particularly useful when integrating a variable other than the radius simplifies the calculation. Additionally, the washer method is defined as the method of the volume of solids that revolves around two curves along the x-axis and y-axis in a bounded region. If you want to Calculate volumes by integrating the difference between the volumes of two enclosing functions. You can use our washer integral calculator particularly useful when the solid has a cavity or hole along the axis of revolution.
Formula used by Cylindrical Shells Calculator
The formula of the shell method which is used by our shell method calculator for the calculations is given below,
$$ V \;=\; \int_{a}^{b} 2\pi x f(x) dx $$
Here 2𝜋x shows the circumstances of a circular object
f(x) represents the height of the shell,
d(x) thickness of the shell.
a,b are the upper and lower limits.
Rules of Shell Method
There are different kinds of formulas for the shell method depending on the given function axis coordinates of curves.
About the y-axis
Revolving the area under the curve of f(x) as y=f(x).
$$ Volume \;=\; V \;=\; 2 \pi \int x f(x) dx $$
About the x-axis
Revolving the area under the curve of f(y) as x=f(y).
$$ Volume \;=\; V \;=\; 2 \pi \int y f(y) dy $$
Between two curves about the y-axis
Revolving the area between two same curves f(x) and g(x)
$$ Volume \;=\; V \;=\; 2 \pi \int x \Biggr[ f(x) - g(x) \Biggr] dx $$
Between two curves about the x-axis
Revolving the area between two similar curves f(y) and g(y)
$$ Volume \;=\; V \;=\; 2 \pi \int y \Biggr[ f(y) - g(y) \Biggr] dy $$
Between two curves about x = h
Revolving the area between two curves f(x) and g(x) and h is the height of the shell
$$ Volume \;=\; V \;=\; 2 \pi \int (x - h) \Biggr[ f(x) - g(x) \Biggr] dx $$
Between two curves about y = k
Revolving the area between two curves f(y) and g(y), k is the height of the shell.
$$ Volume \;=\; V \;=\; 2 \pi \int (y - k) \Biggr[ f(y) - g(y) \Biggr] dy $$
To find the functions f(y) and g(y) defining the outer and inner curves needed for this calculation, you can use our area between the curves calculator to determine the bounded region.
Evaluation process in Shell Method Calculator
The Cylindrical shell calculator is mostly used in calculus to evaluate the volume of solids of revolution in a bounded region about a line along its axis of rotation. When you give input to the calculator, it checks the given function whether its surface area revolves around two curves(it may be similar or different curves).
Then shell method formula calculator identifies the function behavior as it starts the integration process after solving the given function according to the rules of the shell method. At last, it applies the upper and lower limits on a given problem to get an accurate solution.
It gives the outputs of the numerical value of the volume of solid and indefinite integral for the given function. Further, for similar calculations with different numerical integration techniques, you can utilize our trapezium rule calculator to achieve precise results. Additionally, this calculator offers an efficient method for estimating integrals, providing valuable insights into mathematical analyses involving various functions and regions.
Example of Shell Method:
Let us see an example of the cylinder as a practice in the shell method calculator.
Example:
$$ 2 \pi \int_{-1}^{1} x(3x^3 + 2x^2) dx $$
Solution:
Determine the definite integral,
$$ 2\pi \int_{-1}^{1} x \Biggr(3x^3 + 2x^2 \Biggr) dx $$
Expand the integrand x(3x3 + 2x2 )gives 3x4 + 2x3:
$$ 2 \pi \int_{-1}^{1} x \Biggr(3x^4 + 2x^3 \Biggr) dx $$
Integrate the sum and factor out the constants,
$$ 6 \pi \int_{-1}^{1} x^4 dx + 4\pi \int_{-1}^{1} x^3 dx $$
The antiderivative of x4 is x5/3:
$$ \frac{6\pi x^5}{5} \Biggr|_{-1}^{1} + 4\pi \int_{-1}^{1} x^3 dx $$
Calculate the antiderivative at limits,
$$ frac{6\pi x^5}{5} \Biggr|_{-1}^{1} \;=\; \frac{6\pi 1^5}{5} - \left(\frac{6}{5} \pi (-1)^5 \right) \;=\; \frac{12\pi}{5} $$
$$ \frac{12\pi}{5} + 4\pi \int_{-1}^{1} x^3 dx $$
Since x3 is an odd function and the interval [-1, 1] is symmetric about 0 so,
$$ \frac{12\pi}{5} $$
Thus it is the final solution of our function with specific limits. Further, to explore numerical integration methods such as Simpson's Rule, which are useful for approximating integrals like the one mentioned above, you can utilize the Simpson's Rule calculator. Our calculator offers an alternative approach to achieve precise outcomes when tackling intricate functions or areas, enriching your comprehension and problem-solving skills.
How to use the Cylindrical Shell Calculator?
An online shell method calculator finds the volume of the revolution of solid objects if you follow a simple process. These steps are
Step 1:
Enter the given function in the respective field.
Step 2:
Enter the upper and lower limit of integral in its required function.
Step 3:
Review your particular function before clicking on the calculate button.
Step 4:
Click on the “Calculate” button to get the shell problem result.
If you need to calculate the area using numerical methods, such as the Midpoint Rule, you can use our Midpoint Rule Calculator for a more accurate approximation.
Result obtained from the Shell Calculator
You will get instant results of the required function in the shell volume calculator. It also gives some other options with solutions. It may contain:
For similar quick calculations, you can use the midpoint rule approximation calculator to estimate integrals efficiently. It's a handy tool that can provide accurate estimates of integrals using the midpoint rule method, saving you time and effort in your mathematical analyses.
- In the first option, the definite integral gives the value of volume in numbers.
- In the second option a solution with possible steps of definite integral.
- Next box indefinite solution shows with possible steps.
- Click on the “Recalculate” button for more calculations on the shell method tool.
Advantages of Shell Method Formula Calculator
Our cylindrical shells calculator will give you multiple benefits in solving shell problems of two radii over a bound region in a simple manner. These benefits are:
Additionally, the calculator's efficiency saves time, especially in engineering and calculus studies where rapid and accurate volume determinations are crucial. Another helpful tool to save time is the riemann sum to integral calculator. This calculator can make your calculations much easier and faster, especially when dealing with complex mathematical analyses.
- The shell method calculator saves your time and energy from doing the lengthy process.
- This tool integrates the given function with step-wise calculation for the volume of solids.
- Our cylindrical shell calculator has a simple design, anyone can access it.
- Shell volume calculator can operate from any device like a laptop, or tablet through the internet.
- It will provide a detailed solution with steps in no time.
- Our calculator will give a precise shell problem result without any errors.