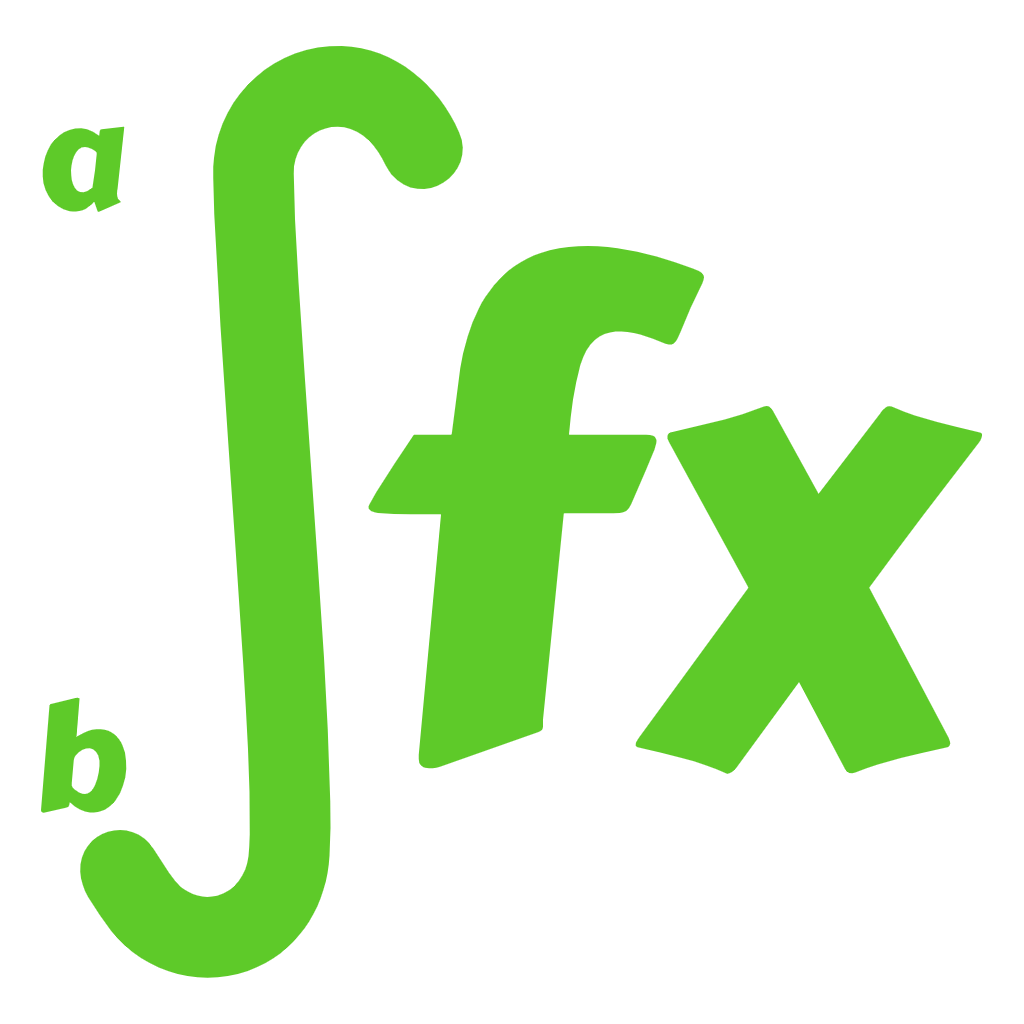Introduction to Disk Method Calculator
The disc method calculator is an online calculator that helps to calculate the volume of spherical objects that rotate in two or three dimensions. This tool uses the disc method formula to give a solution to compute the complex problems for the circular structure of small objects like discs within a minute.

If you are facing difficulty in solving disk method problems, then you can use this disk washer method calculator for the volume of the revolving curve through the integration process.
So Disc method calculator help you computes volume of solids of revolution without cavities, integrating cross-sectional areas of infinitesimally thin disks perpendicular to the axis of rotation. Addionally, if you need to calculating the volume of solids of revolution with cavities or holes, you will use our volume of washer calculator involves integrating the difference in areas between two concentric circles (washers) perpendicular to the axis of rotation.
What is the Disc Method?
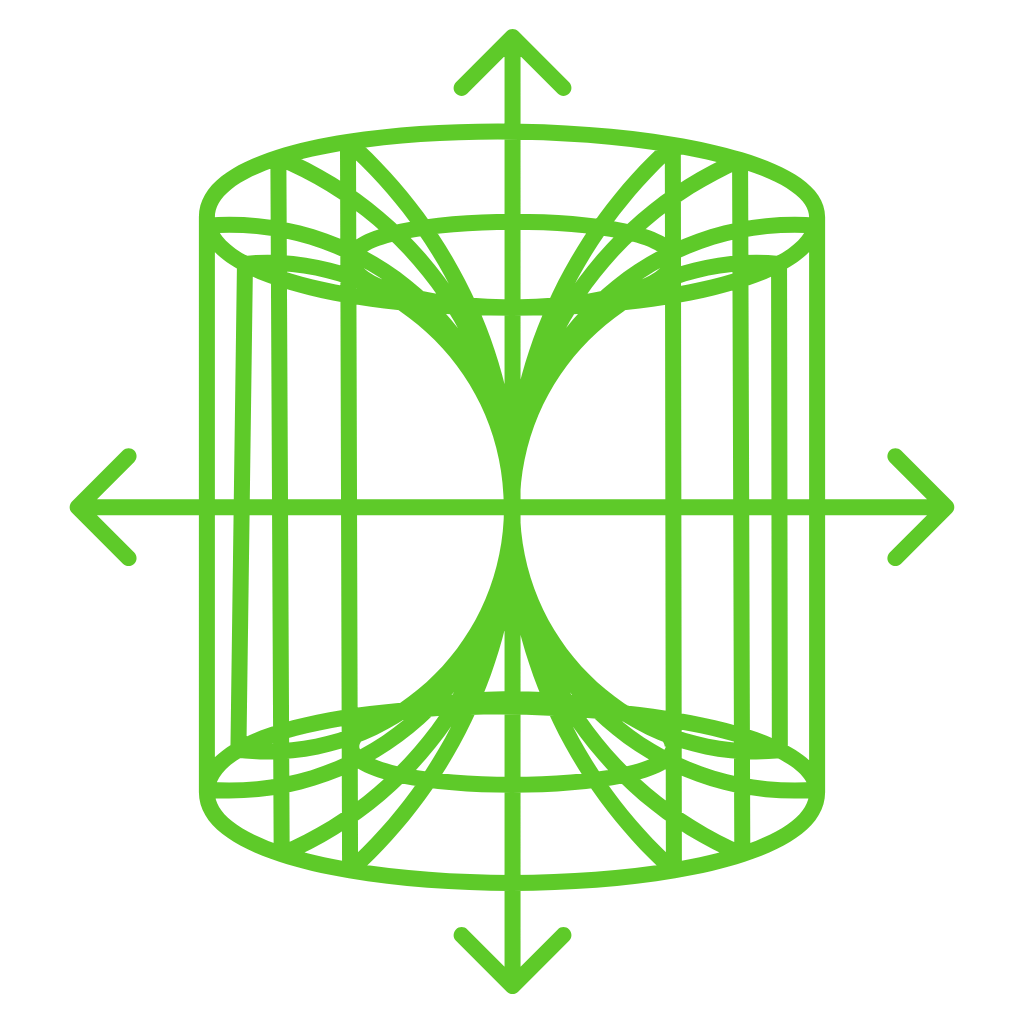
The disc method is an integration method for estimating the volume of solid material of revolution in three dimensions. It is commonly known as the disc method, the volume of a solid method.
The Disc Method is a technique used in calculus to find the volume of a solid of revolution. It involves slicing the solid into thin discs perpendicular to the axis of revolution and summing their volumes. The volume of each disc is calculated using the formula for the area of a circle (πr2)where r represents the radius of the disc.
Addionally, for computations using alternative methods, such as the Shell Method, you can use our cylindrical shell method calculator for efficient volume calculations. Our calculator simplifies volume computations by employing the shell method, which involves summing the volumes of hollow cylindrical shells.
Formula Behind the Disc Method Calculator
Let's see the formula of the disc method used by our disk washer calculator,
$$ V \;=\; \pi \int_{a}^{b} \Biggr[ f( x ) \Biggr]^2 dx $$
Where,
f(x) is the radius of the disc function,
a,b shows the upper and lower limits.
v shows the volume of revolving of the disc along its x-axis.
dx is the height of the disc along the x-axis.
Additionally, for numerical approximation of definite integrals using methods like the Riemann sum, you can use our riemann sum calculator for efficient and accurate estimations. Our calculator is particularly useful when dealing with functions that are difficult to integrate analytically or when analytical methods are not feasible
Working Process of Disk Method Calculator
In the volume of a disk calculator, the disc method formula determines the cross-sectional area and volume of the revolution of complex functions of different shapes.
When you enter the function f(x) along with the upper and lower into the volume of disk calculator, then it starts to recognize the problem as it works according to the formula of the disc method.
Then it uses the integration process to calculate the given definite integral problem.
After integration limits are applied and their limit function solution is multiplied by the pi value. Resultantly, it will provide an accurate solution instantly without any struggle to get a solution.
In two-dimensional shapes like circles around a line or axis, tri-solids contain circular discs and cones, cylinders, etc.
Our disc method calculator is beneficial for students, researchers, and engineers who do not have enough time to solve small circular shapes like disc problems with their axis of rotation.
Additionally, for efficient approximation of definite integrals, you can utilize our trapezoidal rule calculator, which provides accurate results using the trapezoidal rule method. Our calculator is particularly useful for numerical integration tasks, offering a reliable approach to approximate the area under curves.
Now let's under the working on the disc method rule with an example.
Example of Disc Method
Let's discuss an example of the disc method solved by the Disk method calculator.
Example:
$$ \pi \int_{-1}^{2} \Biggr[ (x - 2)^2 - (-2)^2 \Biggr] dx$$
Solution:
$$ \pi \int_{-7}^{2} \Biggr( -4 + (-2 + x)^2 \Biggr) dx \;=\; 207 \pi \approx 650.31 $$
The steps are given below,
Calculate the definite integral,
$$ \pi \int_{-7}^{2} \Biggr( (x - 2)^2 - 4 \Biggr) dx $$
Now integrate the sum term by term and factorize the constants:
$$ \pi \int_{-7}^{2} (x - 2)^2 dx + -4 \pi * \int_{-7}^{2} 1dx $$
For the integrand (x - 2)2, substitute u = x - 2 and du = dx.
This gives a new upper bound u = 2-2 = 0, and lower bound u = -2 -7 = -9.
$$ \pi \int_{-9}^{0} u^2 du + -4\pi * \int_{-7}^{2} 1dx $$
Apply the fundamental theorem of calculus, the antiderivative of u2 is u3/3.
$$ \frac{\pi u^3}{3} \Biggr|_{-9}^{0} + -4\pi * \int_{-7}^{2} 1dx $$
Calculate the antiderivative at the limits and subtract.
$$ \frac{\pi u^3}{3} \Biggr|_{-9}^{0} \;=\; \frac{\pi 0^3}{3} - \Biggr( \frac{1}{3} \pi (-9)^3 \Biggr) \;=\; 243 \pi $$
$$ 243 \pi + -4\pi * \int_{-7}^{2} 1dx $$
By applying the fundamental theorem of calculus, the antiderivative of 1 is x:
$$ 243 \pi + (-4 \pi x) \Biggr|_{-7}^{2} $$
Calculate the antiderivative at the limits and subtract,
$$ (-4 \pi x) \Biggr|_{-7}^{2} \;=\; (-4 \pi 2) - (-4 \pi (-7)) \;=\; -36 \pi $$
$$ 207 \pi $$
This approach gives us the ultimate answer to our problem, considering specific starting and ending points. Additionally, for numerical integration tasks involving more complex shapes, you can use our Simpson's approximation calculator for accurate volume computations. Our calculator also employs Simpson's Rule, a numerical integration method that provides precise approximations for definite integrals by fitting quadratic functions to small intervals of the function being integrated.
How Does the Disk Washer Method Calculator Work?
Disk method calculator works after taking function value from the user as input and calculates it if you follow some simple steps. These steps are:
- Enter your function in the form of f(x), and g(x).
- Add the upper and lower limits in their respective box.
- Click on the “Calculate” button to get a solution.
The Result Obtained from the Disk Washer Calculator
Once you add the correct equation in our disk washer method calculator, it will instantly compute the disc volume problem. You will get the given function solution in the form of:
Further, For computations involving the area between two curves calculator, our calculator provides quick and reliable solutions, enhancing productivity and accuracy in geometric analyses.
- In the first box solution of the definite integral function is shown.
- In the second box, the possible immediate option shows a step-by-step definite integral.
- The next box shows the indefinite integral result and other possible steps of the indefinite integral function.
- Click on the “Recalculate” button to practice more examples of disc method problems.
Conclusion
The disk washer calculator makes the evaluation process of the disc method simple and easy for students as well as engineers to find the volumes of revolution without any mistakes. If you calculate this type of complex problem manually, it takes too much time. Disk method calculator helps a user give precise results every time whenever you need it.
Additionally, for efficient approximation of definite integrals using midpoint approximation, you can explore our midpoint rule calculator, which provides accurate results with the midpoint rule method. Our calculator is particularly useful for numerical integration tasks, offering a reliable approach to approximate the area under curves with reduced computational effort.