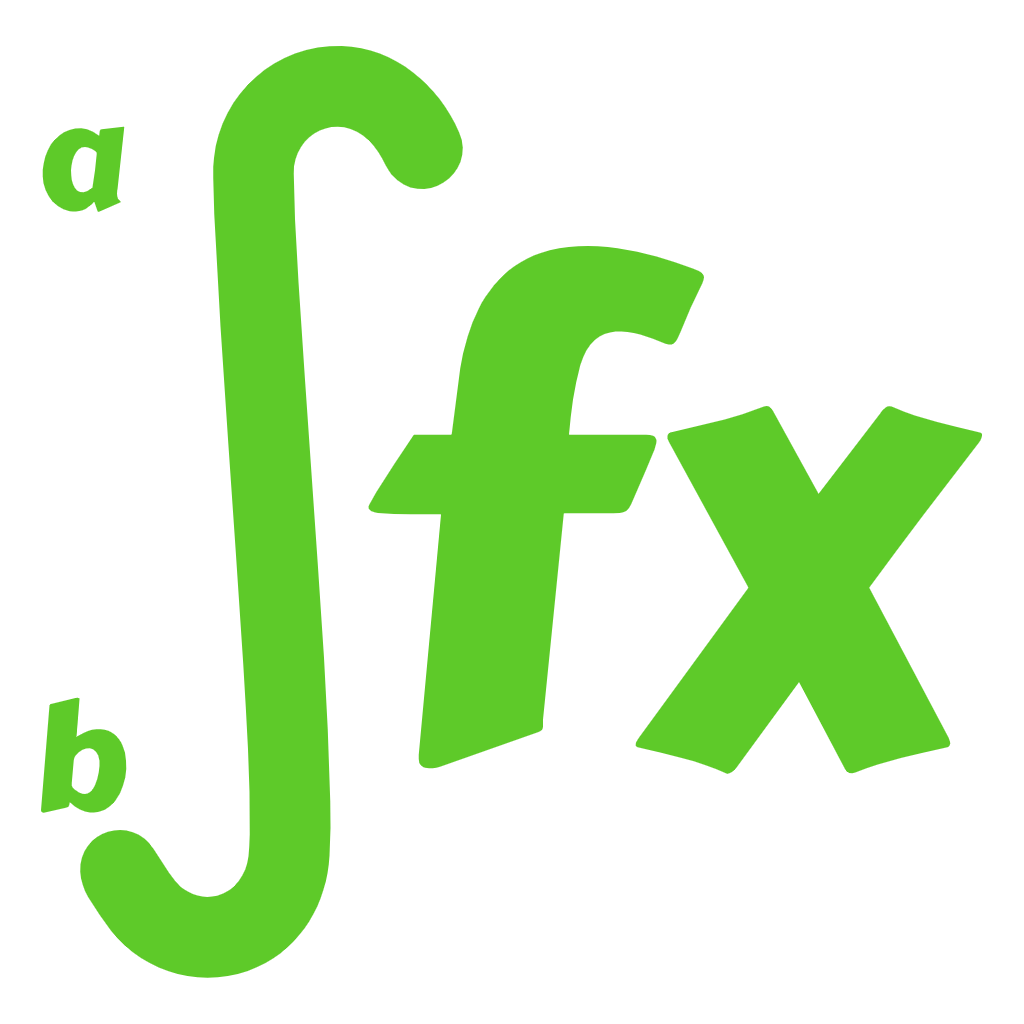Introduction to Antiderivative Calculator with Steps
Antidifferentiation calculator is an online tool that helps you to find the solution of an antiderivative function whether it belongs to the definite or indefinite type.

It is used to evaluate the displacement under the graph in a bounded or unbounded region. We introduce this antiderivatives calculator with advanced algorithms that give every detail of the antiderivative function to enhance the understanding of the user.
So Antiderivative calculator help you to finding the antiderivative of a given function. Additionally, if you need to evaluate triple integrals, check out our triple intergral calculator for computing integrals over three variables.
What is the Antiderivative?
Antiderivative can be defined as the area under the curve of a graph function. The process of the antiderivative in the inverse of the derivative function is called integration. The antiderivative of the function to the variable x is denoted as ∫ f (x) dx.
It has two types:
A definite antiderivative, also known as the definite integral, calculates the net accumulation of a function's values over a specified interval. It involves finding the antiderivative (indefinite integral) of the function and then evaluating it at the upper and lower bounds of the interval, subtracting the result at the lower bound from the result at the upper bound.You can explore more about definite integrals and even compute them using a integrate with limits calculator.
An indefinite antiderivative, also known as an indefinite integral, is the reverse process of differentiation in calculus. It aims to find a family of functions whose derivative matches a given function. This process involves adding a constant term, known as the constant of integration, to represent all possible antiderivatives of the original function.You can learn more about indefinite integrals and even calculate them using a handy tool called an integration calculator indefinite.
- Definite antiderivative
- Indefinite antiderivative
Formula Used by the Antidifferentiation Calculator
The formula used by the anti derivative calculator for antiderivative functions for definite or indefinite is given as,
For Indefinite integral:
The indefinite integral area between curves without specific bounds is like a definite integral.
$$ \int f(x)dx \;=\; F(x) + C $$
For Definite Integral:
The definite integral, denoted by f(x)dx, represents the area between the curve of the function along with the upper and lower limits.
$$ \int_{b}^{a} f(x)dx \;=\; F(b) - F(a) $$
If you want to calculate integrals, you can also use our curve integral calculator for precise results. It also facilitates the calculation of definite integrals, representing the accumulation of quantities such as distance, velocity, or mass over a given range.
Evaluation Behind our Antiderivative Calculator
An anti differentiation calculator evaluates integral functions with the appropriate rules and techniques for integration like the power rule, sum rule, or the rule that is suitable according to the given function.
However, some antiderivative functions are complex and do not give solutions from direct formulas. This antidifferentiation calculator used other methods of integration like substitution, by parts, or partial fraction methods because it has advanced algorithms of the integral method.
When you give input in an antiderivatives calculator it will check the type of function that which method needs to get the given function results easily. After the integration process, it gives a solution and adds a constant of integration C.
In the case of definite after integration, it applies the upper and lower limit values and gives a result without a constant C.
Our tool can manage all types of complex functions that help you to learn a deep understanding of antiderivative functions, especially for those who need more knowledge of integral functions.If you're interested in exploring more advanced calculations, you can also try our multiple integration calculator for evaluating integrals over two variables.
Let us see an example of an anti derivative calculator working to get more clarity on this concept during calculation.
Example of Antiderivative Function
An example of an antiderivative function and its solution for showing how our antiderivative calculator solves problems is given,
Example:
$$ \int \Biggr(x^2 + 5x - 7 \Biggr) dx $$
Solution:
The indefinite integrals are,
$$ \int \Biggr(x^{2} + 5x - 7 \Biggr) dx \;=\; \frac{x^3}{3} + \frac{5x^2}{2} - 7x + constant $$
First, take the integral
$$ \int \Biggr(x^2 + 5x -7 \Biggr) dx $$
Integrate the sum term by term and factor out the constants,
$$ \int x^2 dx + 5 \int xdx - 7 * \int 1dx $$
Putting the integral of x2;
$$ \frac{x^3}{3} + 5 \int xdx - 7 * \int 1dx $$
Putting the integral of x which is x2 / 2
$$ \frac{5x^2}{2} + \frac{x^3}{3} - 7 * \int 1dx $$
The integral of 1 is x:
$$ \frac{x^3}{3} + \frac{5x^2}{2} - 7x + constant $$
So, this expression gives us the ultimate solution for our function, especially when we have specific limits. If those limits are finite, you might want to consider using an converge or diverge calculator integral. Improper integrals are usually handled by either taking limits as the interval stretches to infinity or by breaking down the integral into finite segments. This approach helps manage integrals that might pose challenges due to infinite boundaries or singularities within the interval.
How to Use an Antiderivatives Calculator?
For the evaluation of anti differential functions in the antiderivative calculator with steps, you need to follow some steps to get the solution for your particular function. These steps are:
Step 1:
Enter your function in the input field and choose an integral variable.
Step 2:
In the case of the definite integral you do not need to give limit values.
Step 3:
In the case of a definite integral function enter the upper and lower limit.
Step 4:
Click the “Calculate” button to get the antiderivative function solution.
Results Obtained from the Anti Derivative Calculator
You can get results instantly after putting the antiderivative function in the antiderivative calculator. It gives a few extra options
In the first box, the solution given along with the given input function
In the next box possible steps option if you click on it you will get results with steps
Press Recalculate for example practice.
Moreover, we also offer a line integral online calculator, which enables users to compute line integrals efficiently. Line integrals are essential in various fields, including physics and engineering, for calculating quantities such as work done by a force along a curve or flux through a curve.
Advantages of our Anti Differentiation Calculator
Our antidifferentiation calculator will give multiple benefits when you use it for finding integral functions. These advantages are:
These advantages make our Anti derivative Calculator a valuable tool for students, educators, and professionals working with calculus and related fields.Moreover, visit our website calculate integration online for being attached with the variety of calculus tools.
- The antiderivatives calculator is a reliable tool as it gives precise solutions
- Our anti derivative calculator provides results quickly which saves your valuable time
- You can learn integral concepts with explanations for understanding calculus.
- You can easily access our calculator through any browser on your laptop, computer, or tablet.
- Our antiderivative calculator with steps is a free-of-cost tool you do not need any fee to use it.
- You can use it for practice because you can do unlimited calculations.